A Fórmula de Bháskara é um dos pilares fundamentais da matemática, especialmente no campo da álgebra. Utilizada para resolver equações quadráticas, ela se destaca por permitir encontrar as raízes de uma equação na forma ax²+bx+c=0.
Dessa forma, ao aplicar a fórmula, você consegue determinar as soluções para uma ampla variedade de problemas quadráticos. Assim, compreender e dominar a Fórmula de Bháskara é essencial para resolver eficientemente equações quadráticas e enfrentar desafios matemáticos com confiança.
O Que é a Fórmula de Bháskara?
A Fórmula de Bháskara é um método para resolver equações quadráticas, sendo equações de segundo grau. Uma equação quadrática tem a forma geral ax² + bx + c = 0, onde a, b e c são coeficientes reais, e a≠0. A fórmula é especialmente útil porque oferece uma solução direta para encontrar os valores de xxx que satisfazem a equação.
Desenvolvida pelo matemático indiano Bháskara II no século XII, essa fórmula é uma ferramenta poderosa que tem sido amplamente utilizada e estudada ao longo dos anos. Ela é valorizada não só pela sua eficiência, mas também pela sua simplicidade.
Como a Fórmula de Bháskara Funciona
Para aplicar a Fórmula de Bháskara, você precisa dos coeficientes da equação quadrática. A fórmula é expressa como:
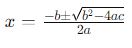
Aqui, 
é chamado de discriminante. O discriminante é crucial porque determina o número e o tipo de soluções da equação. Se o discriminante é positivo, a equação tem duas soluções reais distintas. Se é zero, há exatamente uma solução real, e se é negativo, as soluções são complexas.
Derivação da Fórmula de Bháskara
A Fórmula de Bháskara é um dos métodos mais eficazes para resolver equações quadráticas. Para compreender verdadeiramente como aplicar essa fórmula, é essencial conhecer sua derivação. A derivação não apenas revela a lógica por trás da fórmula, mas também ajuda a entender como ela se ajusta a diferentes tipos de equações. Exploremos a derivação da fórmula passo a passo.
Partindo da Equação Quadrática
Comecemos com a equação quadrática padrão, que tem a forma:
ax² + bx + c = 0
O objetivo é encontrar as raízes dessa equação, ou seja, os valores de x que tornam a equação verdadeira. Para fazer isso, utilizamos o método do completamento de quadrados. Primeiro, dividimos toda a equação por a (desde que a≠0), para simplificar o cálculo. Assim, obtemos:
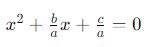
Completando o Quadrado
O próximo passo é completar o quadrado. Começamos isolando o termo constante. Subtraímos c/a de ambos os lados:
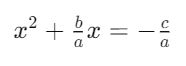
Agora, precisamos transformar o lado esquerdo em um quadrado perfeito. Para isso, adicionamos e subtraímos (b/2a)² no lado esquerdo:
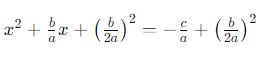
O lado esquerdo da equação agora pode ser reescrito como um quadrado binomial:
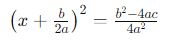
Isolando o x
Para encontrar x, tiramos a raiz quadrada de ambos os lados:
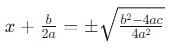
Simplificando a raiz quadrada, obtemos:
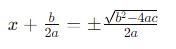
Finalmente, isolamos x subtraindo b/2a de ambos os lados:
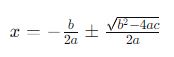
A Fórmula de Bháskara
Reunindo os termos, a fórmula final é:
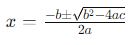
Essa é a Fórmula de Bháskara que conhecemos e utilizamos para resolver equações quadráticas.
Como Utilizar a Fórmula de Bháskara
A Fórmula de Bháskara é uma ferramenta fundamental na resolução de equações quadráticas. Saber como aplicá-la corretamente é essencial para resolver problemas matemáticos de maneira eficiente. Neste guia, exploremos passo a passo como utilizar a Fórmula de Bháskara para encontrar as raízes de uma equação quadrática.
Passo a Passo para Aplicar a Fórmula de Bháskara
Para começar, considere a equação quadrática na forma padrão:
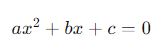
Onde a, b e c são coeficientes reais e a≠0. Utilizemos a Fórmula:
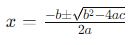
Aqui estão os passos detalhados para aplicar a fórmula:
1. Identifique os Coeficientes
Primeiro, identifique os coeficientes a, b e c da equação quadrática. Por exemplo, se você tem a equação:
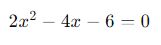
Os coeficientes são:
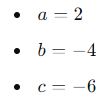
2. Calcule o Discriminante
O discriminante é dado por b²−4ac. Ele ajuda a determinar o tipo de soluções que a equação possui. Calculemos o discriminante para nossa equação exemplo:
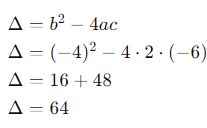
3. Aplique a Fórmula de Bháskara
Substitua os valores de a, b e c na Fórmula de Bháskara:
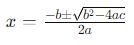
Utilizando o discriminante calculado:
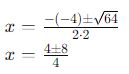
4. Encontre as Raízes
Agora, calcule as duas soluções para x:
Portanto, as raízes da equação 2x²-4x-6 = 0 são x = 3 e x = −1.
Resolução pela Soma e Produto
A resolução de equações quadráticas pode ser abordada por diferentes métodos, e, dentre eles, uma abordagem alternativa à Fórmula de Bháskara é a resolução pela soma e produto das raízes. Esse método se baseia nas propriedades das raízes de uma equação quadrática e pode se mostrar uma ferramenta extremamente útil em várias situações.
Assim, ao explorarmos como utilizar essa abordagem, você poderá descobrir uma maneira eficiente de resolver equações quadráticas sem depender exclusivamente da fórmula tradicional. Dessa forma, compreender e aplicar o método da soma e produto das raízes permitirá ampliar suas opções e técnicas na resolução de problemas matemáticos.
Conceito de Soma e Produto das Raízes
Para uma equação quadrática da forma:
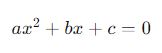
As raízes dessa equação podem ser representadas por x1 e x2. Segundo o teorema de Vieta, para uma equação quadrática, a soma e o produto das raízes mantêm relações diretas e importantes com os coeficientes da equação. Especificamente:
Dessa maneira, o teorema de Vieta fornece uma conexão valiosa entre as raízes da equação e seus coeficientes, oferecendo uma perspectiva adicional para entender e resolver equações quadráticas. Ao explorar essas relações, você pode aplicar uma abordagem alternativa para encontrar soluções e interpretar os resultados de maneira mais eficaz.
Exemplo Prático
Considere a equação quadrática:
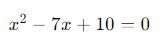
Para resolver utilizando soma e produto, faça o seguinte:
Portanto, dois números que somados resultam em 7 e multiplicados resultam em 10 são x = 2 e x = 5, pois:
2 + 5 = 7
2×5 = 10
Logo, a solução para a equação x²-7x + 10 = 0 é x = 2 e x = 5.
Casos Especiais e Soluções
Quando se trata de resolver equações quadráticas, a Fórmula de Bháskara se destaca como uma ferramenta extremamente útil. No entanto, é importante observar que o comportamento das soluções pode variar significativamente dependendo do valor do discriminante b²−4ac. Nesse sentido, compreender os casos especiais é crucial, pois isso permite interpretar as soluções de maneira mais precisa e resolver problemas matemáticos com maior eficácia.
Dessa forma, ao explorarmos os principais casos especiais, você descobrirá como cada um deles afeta as soluções das equações quadráticas. Assim, ao entender essas nuances, você estará mais preparado para abordar e resolver uma ampla gama de problemas com a precisão e a confiança necessárias.
1. Discriminante Positivo: Duas Soluções Reais Distintas
Quando o discriminante é positivo (b²−4ac>0), a Fórmula de Bháskara resulta em duas soluções reais distintas. Este caso ocorre quando a equação quadrática intersecta o eixo x em dois pontos diferentes. Veja o exemplo na seção anterior.
2. Discriminante Zero: Uma Solução Real
Quando o discriminante é zero (b²−4ac=0), a Fórmula de Bháskara resulta em uma única solução real, conhecida como uma solução real dupla. Este caso ocorre quando a equação quadrática toca o eixo x em um único ponto, formando uma tangência.
Exemplo
Considere a equação quadrática:
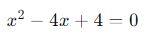
Aqui, os coeficientes são:
Calcule o discriminante:
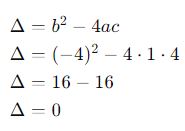
Como é 0, há uma solução real dupla. Aplicando a fórmula:
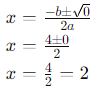
Portanto, a raiz única é x = 2.
3. Discriminante Negativo: Soluções Complexas
Quando o discriminante é negativo (b²−4ac<0), a Fórmula de Bháskara resulta em duas soluções complexas conjugadas. Isso ocorre quando a equação quadrática não intersecta o eixo x e as soluções são números complexos.
Exemplo
Considere a equação quadrática:
x² + 2x + 5 = 0
Aqui, os coeficientes são:
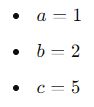
Calcule o discriminante:
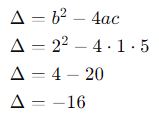
Como Δ<0, há duas soluções complexas conjugadas. Aplicando a fórmula:
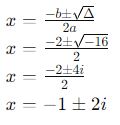
Portanto, as soluções complexas conjugadas são x = −1-2i e x = −1 + 2i.
Conclusão
Dominar a Fórmula de Bháskara é, sem dúvida, essencial para resolver equações quadráticas de forma eficiente e precisa. Neste guia completo, exploramos, detalhadamente, desde a introdução e derivação da fórmula até sua aplicação prática e análise de casos especiais. Ao longo deste percurso, aprendemos a identificar e calcular as raízes de equações quadráticas, compreendendo, assim, como o discriminante influencia o número e o tipo de soluções.
Além disso, ao aplicar a fórmula corretamente e entender os diferentes cenários de discriminante, você está capacitado para resolver uma ampla gama de problemas matemáticos com confiança. A prática contínua, junto à familiarização com os diversos casos especiais, garantirá uma compreensão sólida e uma aplicação eficaz da Fórmula de Bháskara.
Portanto, com esses conhecimentos bem fundamentados, você está adequadamente equipado para enfrentar desafios matemáticos e utilizar a fórmula de maneira eficaz em diversas situações. Assim, continue explorando e praticando, pois isso permitirá aprimorar suas habilidades e alcançar novos níveis de proficiência em álgebra.
