A matemática financeira é um campo fascinante que desempenha um papel crucial na vida de todos, independentemente da profissão ou idade. Por exemplo, desde o cálculo dos juros de um financiamento até o planejamento de uma aposentadoria confortável, os conceitos de matemática financeira são ferramentas essenciais para tomar decisões informadas e eficientes. Assim, este artigo atua como um guia introdutório para aqueles que desejam entender melhor como aplicar esses princípios no seu dia a dia.
A Importância da Matemática Financeira
Vivemos em um mundo onde o dinheiro permeia quase todos os aspectos de nossas vidas. Seja para comprar uma casa, investir em ações ou simplesmente gerenciar o orçamento doméstico, a matemática financeira oferece a base necessária para realizar essas atividades com sucesso.
Além disso, a importância da matemática financeira vai muito além das transações cotidianas. Ela nos ajuda a entender a lógica por trás das taxas de juros, a distinguir entre juros simples e compostos e a analisar como essas taxas impactam nossos investimentos e dívidas. Compreender esses conceitos pode, de fato, fazer a diferença entre prosperar financeiramente e enfrentar dificuldades econômicas.
Aplicações da Matemática Financeira no Cotidiano
Exploremos algumas das aplicações práticas da matemática financeira comuns no nosso dia a dia.
Planejamento Financeiro Pessoal
Uma das aplicações mais importantes da matemática financeira é no planejamento financeiro pessoal. Para muitos, gerenciar finanças pessoais pode ser uma tarefa intimidante. No entanto, com uma compreensão básica de conceitos financeiros, essa tarefa se torna muito mais manejável.
Por exemplo, ao entender como calcular os juros compostos, você pode estimar quanto seu dinheiro crescerá ao longo do tempo se for investido. Isso é fundamental para a criação de um plano de poupança eficaz, seja para a compra de um carro, uma casa, ou para a aposentadoria. Além disso, ao compreender as taxas de juros dos empréstimos, você pode tomar decisões mais informadas sobre quando e como tomar empréstimos, minimizando os custos com juros ao longo do tempo.
Empréstimos e Financiamentos
Outra aplicação prática da matemática financeira é no campo dos empréstimos e financiamentos. Quando você compra uma casa ou um carro, ou mesmo quando usa um cartão de crédito, você está lidando com contratos financeiros que envolvem juros. Saber calcular esses juros e entender os termos do contrato pode evitar surpresas desagradáveis no futuro.
Por exemplo, muitos contratos de empréstimo apresentam uma taxa de juros anual, mas os pagamentos podem ser mensais. Entender como converter a taxa de juros anual para uma taxa de juros mensal é crucial para calcular os pagamentos reais e o custo total do empréstimo ao longo do tempo. Com esses cálculos, você pode comparar diferentes ofertas de empréstimo e escolher a mais vantajosa para sua situação financeira.
Benefícios de Aprender Matemática Financeira
Ao aprofundar seu conhecimento em matemática financeira, você não só melhora suas habilidades de gerenciamento financeiro, mas também aumenta sua capacidade de tomar decisões econômicas informadas. Esse conhecimento é empoderador e pode proporcionar uma maior segurança financeira.
Além disso, a matemática financeira também pode ser aplicada em áreas como investimentos e negócios. Entender como os juros compostos funcionam pode ajudá-lo a avaliar melhor as oportunidades de investimento, enquanto saber calcular o valor presente de fluxos de caixa futuros é essencial para a análise de viabilidade de projetos de investimento.
Conceitos Básicos
A matemática financeira é uma área repleta de conceitos fundamentais que servem como pilares para o entendimento e a aplicação prática no cotidiano. Conhecer esses conceitos básicos é essencial para tomar decisões financeiras informadas e eficazes. Neste artigo, exploremos alguns dos principais conceitos da matemática financeira e como eles se aplicam no dia a dia.
Juros Simples e Compostos
Os juros são um dos conceitos mais importantes na matemática financeira. Eles representam o custo do dinheiro ao longo do tempo, seja em um investimento ou em um empréstimo. Há dois tipos de juros predominantes: simples e compostos.
Juros Simples
Os juros simples são calculados apenas sobre o valor principal inicial, ou seja, a quantidade de dinheiro inicialmente emprestada ou investida. O cálculo dos juros simples segue uma fórmula fundamental:
Por exemplo, se você investir R$ 1.000,00 a uma taxa de juros simples de 5% ao ano por 3 anos, os juros acumulados serão:
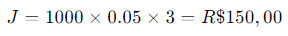
Juros Compostos
Os juros compostos, por outro lado, são calculados sobre o valor inicial mais os juros acumulados de períodos anteriores. Isso quer dizer que a quantia dos juros aumenta de forma exponencial conforme o tempo passa. A fórmula para calcular os juros compostos é:
Por exemplo, se você investir R$ 1.000,00 a uma taxa de juros compostos de 5% ao ano por 3 anos, o montante acumulado será:
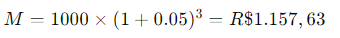
Desconto Simples e Composto
Outro conceito fundamental na matemática financeira é o desconto, que representa a redução do valor de um título ou pagamento futuro para determinar seu valor presente.
Desconto Simples
O desconto simples é calculado da mesma maneira que os juros simples, aplicando uma taxa ao valor futuro para determinar o valor presente. A fórmula é:
Capitalização e Descapitalização
A capitalização e a descapitalização são processos relacionados ao crescimento e à redução do valor do dinheiro ao longo do tempo.
Capitalização
A capitalização refere-se ao processo de calcular o valor futuro de um investimento ou montante ao aplicar uma taxa de juros. Este processo é fundamental para quem deseja entender como seus investimentos podem crescer com o tempo.
Descapitalização
A descapitalização, por outro lado, é o processo de determinar o valor presente de um montante futuro, descontando os juros. Este conceito é crucial para avaliar a viabilidade de investimentos e para entender o valor real do dinheiro ao longo do tempo.
Taxas de Juros
As taxas de juros são um componente crucial na matemática financeira. Elas podem ser categorizadas em várias formas, cada uma com sua aplicação específica.
Taxa Nominal
A taxa nominal é a taxa de juros declarada, geralmente aplicada a um período específico, como um ano. Ela não considera a capitalização dos juros.
Taxa Efetiva
A taxa efetiva considera a capitalização dos juros em períodos menores no prazo de referência da taxa nominal. Por exemplo, uma taxa nominal anual pode ser composta mensalmente, resultando em uma taxa efetiva anual maior.
Taxa Real
A taxa real ajusta-se pela inflação, refletindo o poder de compra real do dinheiro. Para calcular a taxa real, usamos a fórmula:
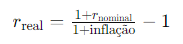
Aplicações Práticas em Matemática Financeira
A matemática financeira não é apenas uma disciplina teórica; suas aplicações práticas estão presentes em diversas situações do nosso dia a dia. Desde a administração de finanças pessoais até decisões empresariais estratégicas, a matemática financeira desempenha um papel crucial. Neste artigo, exploraremos algumas das principais aplicações práticas da matemática financeira e como você pode utilizá-las para melhorar a gestão financeira em diversos contextos. Vamos analisar de forma detalhada como esses conceitos se aplicam no planejamento financeiro pessoal e nas decisões empresariais, oferecendo insights valiosos para otimizar suas finanças e alcançar seus objetivos com maior eficiência.
Planejamento Financeiro Pessoal
Uma das áreas mais impactadas pela matemática financeira é o planejamento financeiro pessoal. Compreender os conceitos e técnicas dessa disciplina é essencial para quem deseja equilibrar suas finanças e alcançar seus objetivos de longo prazo.
Orçamento e Controle de Gastos
O primeiro passo para um bom planejamento financeiro pessoal é criar um orçamento. Um orçamento minucioso possibilita a monitorização das suas entradas e saídas financeiras, permitindo que identifique possíveis áreas de poupança. A matemática financeira ajuda a categorizar e analisar esses dados de forma sistemática.
Investimentos e Poupança
Outro aspecto crucial do planejamento financeiro pessoal é a decisão sobre investimentos e poupança. Entender os conceitos de juros simples e compostos é vital para escolher as melhores opções de investimento.
Suponha que você deseje investir R$ 5.000,00 em um fundo que oferece uma taxa de juros composta de 6% ao ano. Utilizando a fórmula dos juros compostos, você pode calcular quanto esse investimento valerá após 5 anos:
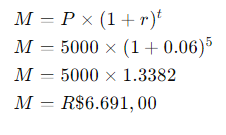
Decisões Empresariais
Além do planejamento financeiro pessoal, a matemática financeira é essencial no mundo dos negócios. Empresas utilizam técnicas financeiras para tomar decisões informadas que impactam diretamente sua lucratividade e sustentabilidade.
Análise de Viabilidade de Projetos
Ao considerar novos projetos ou investimentos, as empresas utilizam a matemática financeira para realizar análises de viabilidade. Uma das ferramentas mais utilizadas é o Valor Presente Líquido (VPL), que ajuda a determinar se um projeto é financeiramente viável ao comparar os fluxos de caixa futuros com o investimento inicial.
A fórmula do VPL é:
Por exemplo, se uma empresa planeja investir R$ 100.000,00 em um projeto que gerará fluxos de caixa de R$ 30.000,00, R$ 40.000,00 e R$ 50.000,00 nos próximos três anos, com uma taxa de desconto de 5%, ela calculará o VPL da seguinte forma:
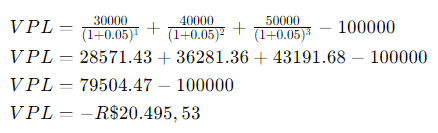
Nesse caso, o VPL negativo indica que o projeto não é viável financeiramente.
Conclusão
A matemática financeira desempenha um papel fundamental em diversos aspectos de nossas vidas, abrangendo desde a gestão das finanças pessoais até a tomada de decisões empresariais estratégicas. Compreender os conceitos e as aplicações práticas dessa disciplina é crucial, pois permite que tanto indivíduos quanto organizações tomem decisões financeiras mais informadas e eficazes.
No âmbito do planejamento financeiro pessoal, por exemplo, podemos criar orçamentos detalhados, controlar gastos, investir de forma inteligente e, assim, garantir uma aposentadoria tranquila. Por outro lado, no contexto empresarial, a análise de viabilidade de projetos e a gestão de dívidas desempenham papéis vitais ao ajudar a maximizar lucros e minimizar riscos, o que, consequentemente, assegura a sustentabilidade a longo prazo.
