As sequências numéricas são, sem dúvida, um dos tópicos mais recorrentes na matemática e desempenham um papel crucial em diversos contextos. Desde problemas cotidianos até aplicações em ciências exatas e sociais, elas se fazem presentes. Entre as sequências mais importantes, destacam-se a P.A. (Progressão Aritmética) e a Progressão Geométrica (P.G.).
Além disso, ambas possuem características particulares e são amplamente utilizadas em provas, como o Enem, bem como em questões mais avançadas de vestibulares. Neste artigo, exploraremos de forma detalhada o que são essas progressões, suas fórmulas principais, exemplos práticos e ainda forneceremos dicas valiosas para resolver problemas com mais eficiência.
Você pode gostar de ler:
- Estatística no ENEM: Dicas Essenciais para Resolver Questões
- Frações, Números Decimais e Dízimas no ENEM: Guia Completo
- Matemática Financeira para Iniciantes: Conceitos e Aplicações
O que é uma Progressão Aritmética (P.A.)
A P.A. (Progressão Aritmética) é uma sequência numérica onde a diferença entre dois termos consecutivos permanece constante. Portanto, esse valor constante é chamado de razão da P.A., e sua fórmula é expressa da seguinte maneira:
Fórmula Geral da P.A.
A fórmula do termo geral da P.A. permite encontrar qualquer termo da sequência. Ela é dada por:
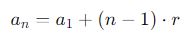
Onde:
- a_n é o enésimo termo da sequência;
- a_1 é o primeiro termo da sequência;
- n representa a posição do termo que se pretende determinar;
- r é a razão da P.A., ou seja, a diferença constante entre os termos consecutivos.
Exemplo Prático de P.A.
Imagine uma sequência no qual o primeiro termo (a_1) é 2 e a razão (r) é 3. Assim, com a fórmula do termo geral, é possível encontrar o valor do quinto termo:
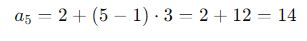
Portanto, o quinto termo da sequência é 14.
Classificação das P.A.s
As P.A.s podem ser classificadas com base na razão:
- P.A. Constante: Quando a razão é 0, todos os termos da sequência são iguais.
- Exemplo: (5, 5, 5, 5…)
- P.A. Crescente: Quando a razão é positiva, a sequência aumenta.
- Exemplo: (3, 6, 9, 12…), onde a razão é 3.
- P.A. Decrescente: Quando a razão é negativa, a sequência diminui.
- Exemplo: (10, 7, 4, 1…), onde a razão é −3.
Soma dos Termos de uma P.A.
Para somar os termos de uma P.A., utiliza-se a seguinte fórmula:
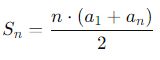
Vemos então que ela é especialmente útil quando o primeiro e o último termo são conhecidos. Se, além disso, soubermos o primeiro termo e a razão, podemos aplicar:
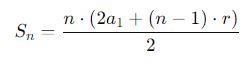
Aplicação Prática: Soma de Termos de uma P.A.
Se quisermos calcular a soma dos 10 primeiros termos de uma sequência onde a_1 = 2 e r = 3, podemos utilizar a fórmula da soma:
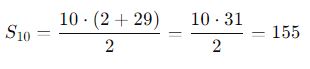
O que é uma Progressão Geométrica (P.G.)
Já a Progressão Geométrica (P.G.) é uma sequência numérica em que cada termo é obtido pela multiplicação do termo anterior por um número constante, assim chamado de razão da P.G.
Fórmula Geral da P.G.
A fórmula do termo geral da P.G. é:
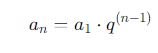
Onde:
- a_n é o enésimo termo;
- a_1 é o primeiro termo;
- q é a razão da P.G.;
- n é a posição do termo.
Exemplo Prático de P.G.
Suponha uma sequência onde o primeiro termo (a_1) é 2 e a razão (q) é 3. Portanto, o quarto termo dessa progressão será:
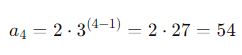
Classificação das P.G.s
Assim como a P.A., as P.G.s também podem ser classificadas com base na razão:
- P.G. Crescente: Quando a razão q > 1, e os termos aumentam progressivamente.
- Exemplo: (2, 6, 18, 54…), onde a razão é 3.
- P.G. Decrescente: Quando 0 < q < 1, os termos diminuem.
- Exemplo: (16, 8, 4, 2…), onde a razão é 1/2.
- P.G. Oscilante: Quando a razão é negativa (q < 0), os termos alternam entre positivo e negativo.
- Exemplo: (2, −4, 8, −16…), onde a razão é −2.
- P.G. Constante: Quando q = 1, todos os termos são iguais.
- Exemplo: (5, 5, 5, 5…), onde a razão é 1.
Soma dos Termos de uma P.G.
Para calcular a soma dos termos de uma P.G., utilizamos a fórmula:
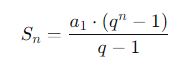
Essa fórmula é válida para P.G.s finitas. Assim, no caso de uma P.G. infinita, com razão 0 < q < 1, a soma é dada por:
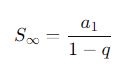
Exemplo Prático: Soma dos Termos de uma P.G.
Se tivermos uma P.G. onde a_1 = 2, q = 3 e queremos calcular a soma dos 4 primeiros termos, portanto, aplicamos a fórmula:
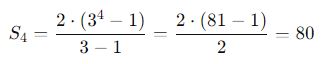
Diferença Entre P.A. e P.G.
Embora P.A. e P.G. sejam tipos de sequências, elas se diferenciam pela forma como seus termos são gerados. Na P.A., adicionamos um valor constante (razão) para encontrar o próximo termo, enquanto, na P.G., multiplicamos por um valor constante (razão).
Tabela Comparativa: P.A. vs P.G.
| Característica | Progressão Aritmética (P.A.) | Progressão Geométrica (P.G.) |
|---|---|---|
| Definição | Diferença constante entre termos consecutivos | Razão constante multiplicativa |
| Fórmula do termo geral | | |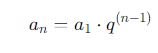
| Soma dos termos | | |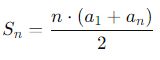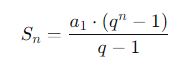
Aplicações Cotidianas de P.A. e P.G.
As progressões se aplicam amplamente em diversas áreas, como economia, engenharia e ciência de dados. Em investimentos, por exemplo, modelam juros simples com uma Progressão Aritmética, enquanto juros compostos seguem uma P.G., o que evidencia a relevância prática desses conceitos.
Dicas para Resolver Questões de P.A. e P.G.
- Entenda a fórmula: Conhecer a fórmula do termo geral facilita, assim, a resolução de qualquer problema envolvendo sequências.
- Identifique o tipo de sequência: Saber se é uma P.A. ou P.G. é fundamental para aplicar as fórmulas corretas e, portanto, resolver corretamente as questões.
- Pratique com questões anteriores: Muitos exames repetem padrões de questões, assim praticar pode te ajudar a identificar esses padrões mais rapidamente.
Exercícios Propostos
- Dada a sequência (3, 6, 9, 12, 15), determine o 10º termo e a soma dos 10 primeiros termos.
- Se uma P.G. tem a_1 = 5 e q = 2, encontre o 6º termo e a soma dos 6 primeiros termos.
Conclusão
Em suma, a Progressão Aritmética (P.A.) é uma ferramenta poderosa na matemática, capaz de descrever fenômenos que ocorrem de forma linear, como o crescimento de salários ou a distribuição de pontos em competições. Compreender a P.A. e sua fórmula é essencial para resolver problemas práticos do cotidiano e acadêmicos, oferecendo uma base sólida para a análise de dados.
Além disso, o domínio da P.A. e suas aplicações facilita a resolução de questões em diversas áreas, como finanças e ciências exatas. Portanto, a prática constante, por meio de exercícios e exemplos do dia a dia, não apenas fortalece o entendimento da P.A., mas também aprimora as habilidades matemáticas. Assim, incentivar o estudo desses conceitos é crucial para desenvolver competências analíticas.
